Quiz 1 Review Sheet
Fall 2016 Note: This is not a comprehensive review. Namely, it does not cover the
cs111/iteratedlibrary, nor does it coverandmapandormap. Examples are minimal; for more in-depth explanations, see the recitation notes.
Primitive Types
Programs are made up of data objects, which are categorized into types. Primitive types are categories of data objects that can't be divided into different types.
Numbers are made up of digits and symbols.
- Examples:
10,3/2,-94.6,pi
- Examples:
Strings are sequences of characters enclosed by a pair of double quotes (
").- Examples:
"hello world","a","10","\"YOLO!\" he screamed."
- Examples:
Booleans are logical values. They are one of:
true(equivalently,#true,#t, or#T)false(equivalently,#false,#f, or#F)
Images
Images are exactly what you think they are. Working with images in Racket typically requires the 2htdp/image teachpack, which can be imported using
(require 2htdp/image)Here are some examples of images:
| Output | Equivalent Code |
|---|---|
(overlay (circle 10 "solid" "red") (circle 20 "solid" "blue")) |
|
(rotate 45 (ellipse 60 20 "solid" "green")) |
|
| copy and pasted from Google Images |
Structs
Structs (also called records) are more complex data types. They can be thought of as custom "templates" for kinds of data.
Define a new struct using
(define-struct <StructType> (<FieldName1> <FieldName2> ... <FieldNameN>))
> (define-struct birthday (day month year))When you define a struct, the following functions also become defined:
| Name | Description | Syntax |
|---|---|---|
| The "Maker" | make-<StructType> |
Creates a new instance of StructType (you can think of it as "filling out" the template) |
| The "Validator" | <StructType>? |
Checks whether some data object is an instance of StructType |
| The "Getter" | <StructType>-<FieldName> |
Gets a particular field value from an instance of StructType |
The exact signatures for each function are:
make-<StructType> : FieldType1 FieldType2 ... FieldTypeN -> StructType
> (define MY_BIRTHDAY (make-birthday 10 "August" 1993))<StructType>? : any -> boolean
> (birthday? MY_BIRTHDAY
true
> (birthday? (make-birthday 5 "June" 1965))
true
> (birthday? 40)
false<StructType>-<FieldName> : StructType -> FieldType
> (birthday-month MY_BIRTHDAY)
"August"
> (birthday-month (make-birthday 5 "June" 1965))
"June"Lists
Lists are collections of data objects.
(list <Item1> <Item2> ... <ItemN>)Lists have types too, denoted using the syntax
(listof <Type>)where <Type> is any of the types we've already seen, or any if the list contains multiple types.
Here are examples of lists and their types:
| Example | Type |
|---|---|
(list 1 2 3 4) |
(listof number) |
(list (circle 10 "solid" "red") (square 40 "outline" "blue")) |
(listof image) |
(list (list 1 2) (list 3 4) |
(listof (listof number)) |
(list 1 2 true) |
(listof any) |
Function Signatures
Functions (also called procedures) are data objects that take input data objects (also called "arguments"), and return a data object output. Each function has a signature indicating the types of its inputs and outputs.
InputType1 InputType2 ... InputTypeN -> ReturnTypeHere are some example signatures:
; regular functions with set input types and orders
even? : number -> boolean
circle : number string string -> image
; functions that take an arbitrary number of inputs of a given type
+ : number ... -> number
string-append : string ... -> string
; functions that take any type
number? : any -> boolean
; functions that take other functions
iterated-overlay : (number -> image) number -> image
map : (a -> b) (listof a) -> (listof b)Basic Order of Operations
In Racket, expressions comprised of function calls are simplified according to the following rule:
Evaluate parentheses first (as deeply nested as necessary), then simplify your way out, working from left to right when multiple expressions are nested at the same level.
Calling Functions
In Racket, we call (or apply) functions using the following syntax:
(<FunctionName> <InputType1> <InputType2> ... <InputTypeN>)To break this syntax down in painstaking detail,
- Opening paren
(tells Racket we are calling a function; <FunctionName>, e.g.+, tells Racket which function;- Space between function name and first input;
- Inputs in order, separated by spaces;
- Closing paren
)tells Racket we are done listing inputs.
Note that function calls are always enclosed in parentheses (). When a function call is evaluated, the call (<FunctionName> ...) gets transformed into its return value.
> (+ 1 1)
2This grammatical rule results in the following behaviors:
If a function and series of arguments are not enclosed in parentheses, Racket will not evaluate the function. It will simply return the function object and its arguments, all separately.
> + 1 1 + ; the function object 1 1- If a non-function is enclosed in parentheses, Racket will try to call it (per the rules of the grammar). If the first chunk after the opening paren is not a function name, Racket will throw the following error:
> (+ (1) 1) function call: expected a function after the open parenthesis, but received 1
- If a non-function is enclosed in parentheses, Racket will try to call it (per the rules of the grammar). If the first chunk after the opening paren is not a function name, Racket will throw the following error:
Using apply
Instead of calling a function directly,
(<FunctionName> <Input1> <Input2> ... <InputN>)we can use apply to pass in a list of inputs:
(apply <FunctionName> (list <Input1> <Input2> ... <InputN>))That is, apply takes two arguments:
, the name of the function to call - (list
... , the inputs with which to call) <FunctionName>, in the correct order.
Some functions, such as +, string-append, and overlay, take an arbitrary number of inputs. That is, their signatures are
+ : number ... -> number
string-append : string ... -> string
overlay : image ... -> imagewith the ellipses ... being the important part.
We use apply to call these types of functions with a list of elements:
> (apply + (list 1 2 3))
6
> (apply string-append (list "thanks" " " "obama"))
"thanks obama"Defining Constants
Constants bind identifiers (or "names") to values.
(define <ConstantName> <ConstantValue>)<ConstantName>is a sequence of non-whitespace characters except for the following:()[]{}"';#|\` (don't memorize this list; basically, it's just any character that would turn the constant name into something else, like a string or function call)- By convention, Racket constants are formatted in
CAPITAL_LETTERSwith underscores separating words.
<ConstantValue>is any value, ranging from primitive objects to complex expressions.
Here are some examples of constant definitions:
; simple primitives
(define FIRST_NAME "sarah")
(define LAST_NAME "lim")
(define YEAR 2016)
; expressions
(define NEXT_YEAR (+ YEAR 1))
(define NICKNAME (string-append (substring FIRST_NAME 0 1)
LAST_NAME))
; defining a struct for the next example; this is NOT a constant
(define-struct contact (first last nickname year-met))
; non-primitive data types
(define ME (make-contact FIRST_NAME LAST_NAME NICKNAME YEAR))
(define IAN (make-contact "ian" "horswill" "dumbledore" YEAR))
(define CONTACTS (list ME
IAN
(make-contact FIRST_NAME "palin" "oh no" 2008)))Constants declared at the outermost level of the program (you can think of this as the "unindented" level) have global scope, meaning they can be referenced from anywhere in the program, including within function definitions.
Lambdas
Lambdas create anonymous functions, i.e. functions without names/identifiers.
(lambda (<Input1> <Input2> ... <InputN>) <Body>)A lambda consists of two parts:
- A sequence of inputs (also known as arguments or parameters), enclosed within parens
() - A function body, some kind of expression.
We can call a lambda using the same old rules of function calls:
; (<FunctionName> <InputType1> <InputType2> ... <InputTypeN>)
> ((lambda (x) (* 2 x)) 5)
10It's generally easier (and much more readable) to define constant names for our functions, so we can reference them later.
; (define <ConstantName> <ConstantValue>)
(define doubler
(lambda (x) (* 2 x)))Scoping
Once we have defined a constant or a function, Racket will automatically plug in <ConstantValue> whenever it sees <ConstantName>.
The scope of a name refers to the parts of a program where this plugging-in behavior works. We've dealt with two examples of scopes thus far:
- Global scope: anything
definedat the outermost level of our program can be referenced from within any scope after the definition. - Function scope: if a lambda
my-cool-functiontakes inputsaandb, thenaandbcan be referenced anywhere within the body of the lambda, including any nested inner lambdas. They cannot be referenced outside ofmy-cool-function.
If a name my-cool-variable is defined once, then _re_defined in some inner scope, the inner redefinition shadows the outer definition, meaning Racket will use the closest definition of my-cool-variable whenever it evaluates our program.
(define HEIGHT 5)
HEIGHT ; 5
(define example-function
(lambda (HEIGHT) ; the name HEIGHT has been redefined within example-function
(+ HEIGHT 1)))
(example-function 30) ; 31Local Scoping
It's a good practice in software engineering to make all your definitions as private as possible, to avoid leaking them out to other parts of the program.
Suppose we have a helper function or variable specific to a particular function. We can use local to create scopes for these helpers, while keeping them from leaking to other functions.
(local [<Definition1> <Definition2> ... <DefinitionN>] <Body>)The keyword local has two parts:
- A list of definitions enclosed within square brackets,
- A body where these definitions, along with any definitions outside the
local, can be referenced.
The definitions in square brackets cannot be referenced outside the local body.
Variable shadowing applies to local definitions as well. If my-cool-name is defined globally, and redefined within a local scope, then the body of the local will use the definition in the square brackets instead of the global definition.
Conditionals
Conditionals allow our programs to "branch" based on a series of logical cases.
if
The simplest conditional branch is if.
(if <Condition> <ThenExpression> <ElseExpression>)<Condition>is a boolean expression<ThenExpression>and<ElseExpression>are expressions or primitive values of any type.
When Racket encounters an if, it does the following:
- Evaluate
<Condition>by simplifying it down to eithertrueorfalse - Based on the result of step 1,
- If
true, jump to<ThenExpression> - If
false, jump to<ElseExpression>
- If
> (if (even? 2) "2 is even" "2 is odd")
"2 is even"
> (if (> 3 5)
"3 is greater than 5"
"3 is not greater than 5")
"3 is not greater than 5"and
We use the logical operator and to determine if a series of boolean expressions are all true.
(and <Boolean1> <Boolean2> ... <BooleanN>) -> Boolean(and A B) is true if and only if A is true and B is true.
| Example | Result |
|---|---|
(and true true) |
true |
(and true false) |
false |
(and false true) |
false |
(and false false) |
false |
or
We use the logical operator or to determine if at least one expression in series of boolean expressions is true.
(or <Boolean1> <Boolean2> ... <BooleanN>) -> Boolean(or A B) is true if and only if A is true or B is true.
| Example | Result |
|---|---|
(or true true) |
true |
(or true false) |
true |
(or false true) |
true |
(or false false) |
false |
not
We use the logical operator not to "flip" a single boolean value, i.e. get its logical opposite.
(not <Boolean>) -> BooleanThe table for not is simple:
| Example | Result |
|---|---|
(not true) |
false |
(not false) |
true |
Lambda Abstractions
It's useful to be able to perform operations on entire lists of data, rather than one object at a time. Racket gives us several functions to use. Here's an high-level summary of what each one does:
| Function | Description | Image |
|---|---|---|
map |
Transforms a list by applying a function to each item | 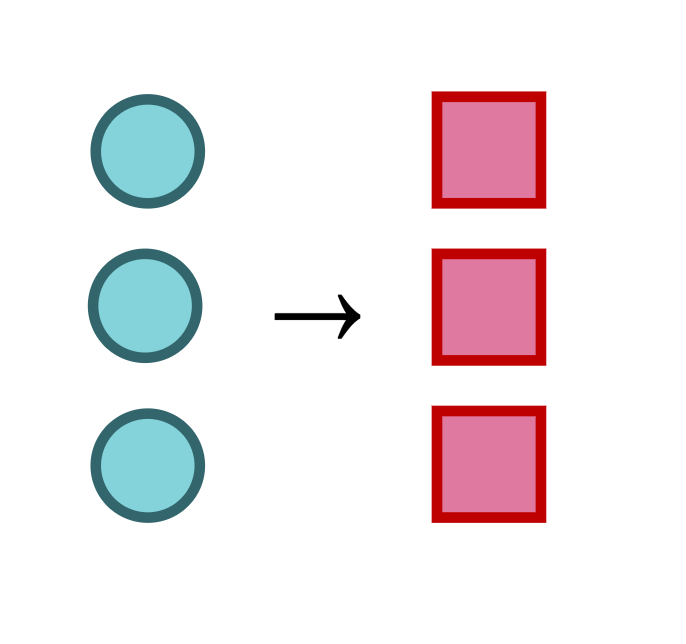 |
filter |
Filters out items that fail some test | 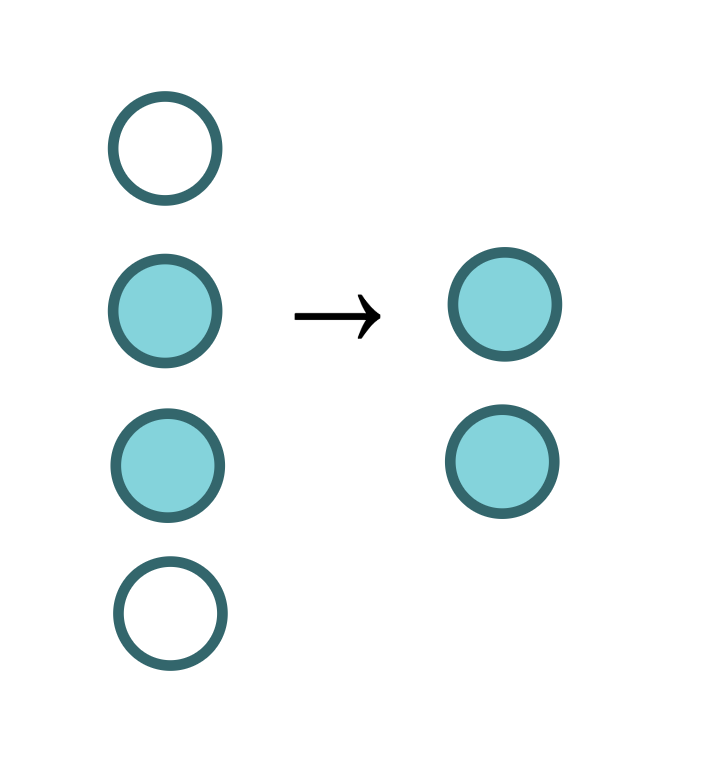 |
foldl and foldr |
Combines everything in a list into a single item | 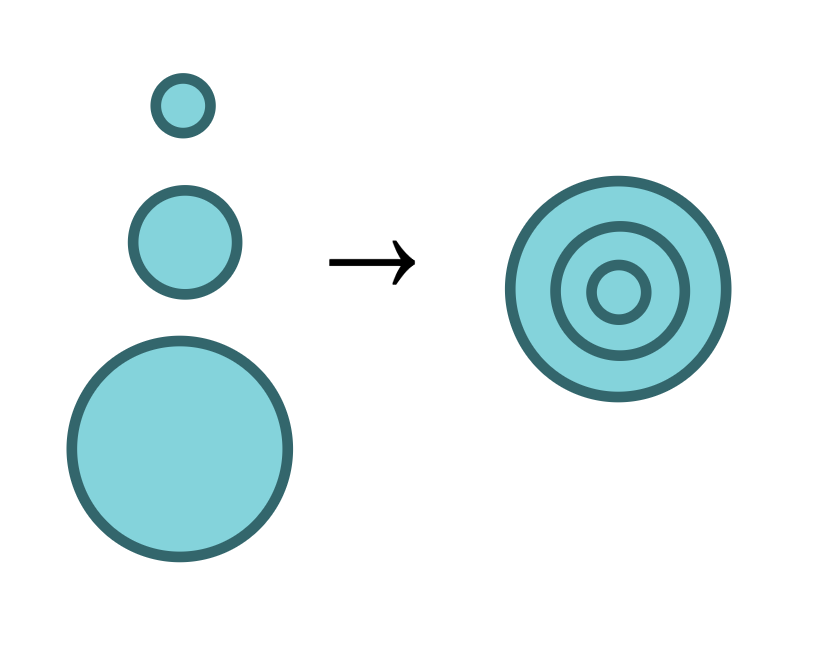 |
map
The map function allows us to transform a list.
map : (X -> Y), (listof X) -> (listof Y)It takes two inputs:
- A function with signature
X -> Y, i.e. a function that takes an input of typeXand returns an input of typeY, and - A list of elements of type
X
and "maps" the function over each item in the input list, returning a list of elements of type Y.
> (map even? (list 1 2 3 4 5 6))
(list false true false true false true)filter
The filter function allows us to filter out elements of a list that don't match a given criteria.
filter : (X -> boolean), (listof X) -> (listof X)It takes two inputs:
- A predicate function, i.e. a function that returns a boolean, and
- A list of elements to filter according to the predicate.
It returns a subset of the original list, consisting of only those elements for which the predicate returned true.
> (filter even? (list 1 2 3 4 5 6))
(list 2 4 6)
> (filter (lambda (s)
(> (string-length s) 1))
(list "a" "aa" "aaa"))
(list "aa" "aaa")foldl and foldr
The fold functions collapses a list into a single object using a given function.
foldl : (X, Y -> Y), Y, (listof X) -> YIt's easiest to think about foldl as "rolling a snowball" through the list. At each item, we use the combiner function to add the current item to the snowball somehow. After we've rolled the snowball all the way through the list, we return the snowball.
Let's unpack the above signature. foldl takes three arguments:
A combiner function
(X, Y -> Y), which will take two inputs: 1.X, the current item from the(listof X)2.Y, the accumulator (our snowball), representing everything we've gotten from combining the previous elements in the listand combine them into the "next"
Y.An initializer of type
Y, which represents the "seed" for our snowball; it's passed to the combiner function whenfoldlprocesses the very first list item.- A list of type
(listof X)that we want to collapse.
foldr works the same way as foldl, except it starts from the rightmost item and snowballs left.
> (foldl - 0 (list 1 2 3 4))
2
> (foldr - 0 (list 1 2 3 4))
-2